SUBTITUSI TRIGONOMETRI

-

YUK JADI KITA AKAN BAHAS SUBTITUSI TRIGONOMETRI LANGSUNG SAJA KE CONTOHNYA.... 

Contoh yang pertama adalah

Substitusi Trigonometri: u = a sin θ

mari kita selesaikan :

Contoh 1 Soal

yuk langsung aja kita bahas

Untuk menggunakan substitusi trigonometri, kita harus melihat bahwa √(9 – x²) merupakan bentuk dari √(a² – u²). Sehingga kita dapat menggunakan substitusi

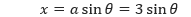
Contoh 1 Subsitusi

Sehingga, persamaan yang menghubungkan variable x dan θ di atas dapat dimodelkan ke dalam segitiga siku-siku sebagai berikut.

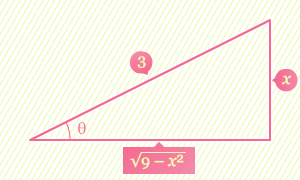
Contoh 1


Dengan menggunakan turunan dan segitiga di atas, kita mendapatkan



Sehingga, dengan menggunakan substitusi dihasilkan

 Contoh 1 Integral


Perhatikan bahwa segitiga pada gambar di pembahasan.

Contoh 1 tersebut, dapat juga digunakan untuk mengubah θ kembali menjadi x sebagai berikut

Cotangen

nah setelah ini langsung saja ke contoh kedua,

Contoh kedua:

Substitusi Trigonometri: u = a tan θ

Tentukan,

Contoh 2 Soal

yuk langsung saja kita bahas 

Misalkan u = 2x, a = 1, dan 2x = tan θ, seperti yang dapat digambarkan sebagai berikut.

Contoh 2

Sehingga, kita mendapatkan

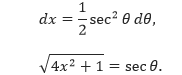
Contoh 2 dx

Dengan menggunakan substitusi trigonometri, didapatkan

Contoh 2 Integral

Selanjutnya kita dapat memperluas penggunaan dari substitusi trigonometri untuk menyelesaikan integral yang memuat bentuk (a² – u²)n/2 dengan menuliskan bentuk tersebut ke dalam

Pangkat Rasional

sumber :

 https://yos3prens.wordpress.com/2014/10/28/teknik-integral-substitusi-trigonometri/2/


Komentar

Posting Komentar

Postingan populer dari blog ini

KOORDINAT POLAR

-
Gambar
  Penjelasan Koordinat Polar Sistem koordinat polar (sistem koordinat kutub) dalam matematika adalah suatu sistem koordinat 2-dimensi di mana setiap titik pada bidang ditentukan dengan jarak dari suatu titik yang telah ditetapkan dan suatu sudut dari suatu arah yang telah ditetapkan. Konversi dari atau ke  koordinat Kartesius Sebuah diagram menggambarkan hubungan antara  sistem koordinat Kartesius  dan polar. Sebuah diagram  menggambarkan hubungan antara  sistem koordinat Kartesius  dan polar. Sebuah kurva dalam bidang Kartesian dapat dipetakan ke dalam koordinat polar. Dalam animasi ini,     dipetakan kepada  .   . Koordinat polar  r  dan  φ  dapat dikonversi ke dalam  sistem koordinat Kartesius   x  dan  y  menggunakan  fungsi trigonometri   sinus  dan  kosinus : Kartesian   x  dan  y  dapat dikonversi ke dalam koordinat polar...
Baca selengkapnya

menghitung volume benda pejal dengan integral

-
Gambar
  LANGSUNG SAJA KITA KE DALAM SOALNYA YA Carilah volume benda pejal dengan persamaan dan batas-batas pada sumbu x dan sumbu y dibawah ini. Jawaban Soal : Untuk mendapatkan gambaran benda pejal yang akan dicari volumenya, kita akan plotkan persamaan z=f(x,y) dari soal dengan batas-batas terhadap sumbu x dan sumbu y tersebut ke dalam grafik ruang dimensi tiga. Kemudian kita akan menghitung volume yang terbentuk diantara persamaan z=f(x,y) dan bidang xy dengan batas-batas sumbu x dan sumbu yang diberikan, yaitu daerah merah. Berikutnya kita akan menghitung volume benda pejal berwarna merah menggunakan integral lipat, dalam hal ini integral lipat dua karena kita akan mengintegralkan terhadap batas-batas di arah sumbu x dan sumbu y. Ingatlah bahwa jika ada batas berupa persamaan maka kita akan mendahulukannya dalam proses integral, dan integral pada lapis terluar baru terhadap batas-batas berupa angka. Pertama-tama kita tuliskan bentuk integral berbatas dengan batas-batas ...
Baca selengkapnya

MENGHITUNG LUAS DAERAH DENGAN INTEGRAL

-
Gambar
  Mencari Luas Daerah yang Dibatasi Kurva – Aplikasi integral dapat ditemukan pada cara mencari luas daerah yang dibatasi kurva. Baik yang dibatasi oleh sebuah kurva atau lebih. Selain itu, aplikasi integral juga digunakan untuk mencari volume benda putar yang merupakan daerah yang dibatasi kurva kemudian diputar 360 o  mengelilingi sumbu x atau sumbu y.        Luas Daerah yang Dibatasi Sebuah Kurva Luas suatu daerah yang dibatasi sebuah kurva dapat dicari menggunakan rumus integral. Pehatikan gambar luas daerah yang dibatasi sebuah kurva dan rumus integral untuk mencari luas daerah tersebut di bawah!       Selain rumus integral untuk mencari luas daerah yang dibatasi kurva yang telah diberikan di atas, terdapat juga aturan penggunaan rumus integral. Berikut ini adalah aturan penggunaan aturan integral dalam mencari luas daerah yang dibatasi oleh kurva.   Luas daerah yang dibatasi kurva f(x) pada selang a dan b di a...
Baca selengkapnya