Turunan Fungsi

-

PENGERTIAN TURUNAN 

Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.

Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan 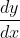  atau   atau y’ dan didefinisikan sebagai :




Pengertian Turunan Fungsi

Turunan Fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalkan fungsi f menjadi f’ yang memiliki nilai tidak beraturan.


Rumus Dasar Turunan dari Turunan Fungsi


Aturan-aturan dalam turunan fungsi ialah:
  1. f(x), menjadi f'(x) = 0
  2. Apabila f(x) = x, maka f’(x) = 1
  3. Aturan pangkat : apabila f(x) = xn, maka f’(x) = n X n – 1
  4. Aturan kelipatan konstanta : apabila (kf) (x) = k. f’(x)
  5. Aturan rantai : apabila ( f o g ) (x) = f’ (g (x)). g’(x))


 contoh soal
    Tentukan turunan pertama dari fungsi berikut:
    a) f(x) = 10x
    b) f(x) = 8
    c) f(x) = 12
  Pembahasan
  a) f(x)   = 10x
      f(x)   = 10x1
      f ‘(x) = 10x1−1
      f ‘(x) = 10x0
      f ‘(x) = 10
 b) f(x)   = 8
     f(x)   = 8x0
     f ‘(x) = 0⋅ 8x0−1
     f ‘(x) = 0

c) f(x)   = 12
    f ‘(x) = 0
sumber : 
https://www.studiobelajar.com/turunan-fungsi/
https://rumusbilangan.com/turunan-fungsi/
https://andikapras17.wordpress.com/2015/05/08/contoh-soal-dan-pembahasan-turunan-fungsi/


Komentar

Posting Komentar

Postingan populer dari blog ini

KOORDINAT POLAR

-
Gambar
  Penjelasan Koordinat Polar Sistem koordinat polar (sistem koordinat kutub) dalam matematika adalah suatu sistem koordinat 2-dimensi di mana setiap titik pada bidang ditentukan dengan jarak dari suatu titik yang telah ditetapkan dan suatu sudut dari suatu arah yang telah ditetapkan. Konversi dari atau ke  koordinat Kartesius Sebuah diagram menggambarkan hubungan antara  sistem koordinat Kartesius  dan polar. Sebuah diagram  menggambarkan hubungan antara  sistem koordinat Kartesius  dan polar. Sebuah kurva dalam bidang Kartesian dapat dipetakan ke dalam koordinat polar. Dalam animasi ini,     dipetakan kepada  .   . Koordinat polar  r  dan  φ  dapat dikonversi ke dalam  sistem koordinat Kartesius   x  dan  y  menggunakan  fungsi trigonometri   sinus  dan  kosinus : Kartesian   x  dan  y  dapat dikonversi ke dalam koordinat polar...
Baca selengkapnya

menghitung volume benda pejal dengan integral

-
Gambar
  LANGSUNG SAJA KITA KE DALAM SOALNYA YA Carilah volume benda pejal dengan persamaan dan batas-batas pada sumbu x dan sumbu y dibawah ini. Jawaban Soal : Untuk mendapatkan gambaran benda pejal yang akan dicari volumenya, kita akan plotkan persamaan z=f(x,y) dari soal dengan batas-batas terhadap sumbu x dan sumbu y tersebut ke dalam grafik ruang dimensi tiga. Kemudian kita akan menghitung volume yang terbentuk diantara persamaan z=f(x,y) dan bidang xy dengan batas-batas sumbu x dan sumbu yang diberikan, yaitu daerah merah. Berikutnya kita akan menghitung volume benda pejal berwarna merah menggunakan integral lipat, dalam hal ini integral lipat dua karena kita akan mengintegralkan terhadap batas-batas di arah sumbu x dan sumbu y. Ingatlah bahwa jika ada batas berupa persamaan maka kita akan mendahulukannya dalam proses integral, dan integral pada lapis terluar baru terhadap batas-batas berupa angka. Pertama-tama kita tuliskan bentuk integral berbatas dengan batas-batas ...
Baca selengkapnya

MENGHITUNG LUAS DAERAH DENGAN INTEGRAL

-
Gambar
  Mencari Luas Daerah yang Dibatasi Kurva – Aplikasi integral dapat ditemukan pada cara mencari luas daerah yang dibatasi kurva. Baik yang dibatasi oleh sebuah kurva atau lebih. Selain itu, aplikasi integral juga digunakan untuk mencari volume benda putar yang merupakan daerah yang dibatasi kurva kemudian diputar 360 o  mengelilingi sumbu x atau sumbu y.        Luas Daerah yang Dibatasi Sebuah Kurva Luas suatu daerah yang dibatasi sebuah kurva dapat dicari menggunakan rumus integral. Pehatikan gambar luas daerah yang dibatasi sebuah kurva dan rumus integral untuk mencari luas daerah tersebut di bawah!       Selain rumus integral untuk mencari luas daerah yang dibatasi kurva yang telah diberikan di atas, terdapat juga aturan penggunaan rumus integral. Berikut ini adalah aturan penggunaan aturan integral dalam mencari luas daerah yang dibatasi oleh kurva.   Luas daerah yang dibatasi kurva f(x) pada selang a dan b di a...
Baca selengkapnya