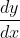catatan harianku

Persamaan yang dapat dituliskan dalam bentuk  y  =  f(x)  disebut persamaan fungsi eksplisit. Sebagai contohnya yaitu : Tidak semua fungsi dapat dituliskan dalam bentuk eksplisit. Contohnya seperti berikut ini:                      Secara umum, fungsi  f(x,y)  =  c , dengan c anggota dari bilangan real disebut persamaan fungsi implisit. Turunan fungsi implisit dilakukan pada fungsi-fungsi implisit tanpa mengubah bentuk fungsi implisit menjadi fungsi eksplisit. Menurunkan fungsi implisit terhadap  x  dapat dilakukan dengan cara seperti berikut ini: 1. Turunkan kedua ruas (ruas kanan dan ruas kiri) terhadap  x. 2. Gunakan aturan rantai 3. Tentukan  dy/dx Aturan rantai adalah sebagai berikut:     1contoh soal :      Pada soal kita mencari bentuk turunan dy/dx dari persamaan x^2+y^2=2x, pada permasalahan ini dapat kita seles...

PENGERTIAN TURUNAN  Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi. Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan    atau    atau y’ dan didefinisikan sebagai : Pengertian Turunan Fungsi Turunan Fungsi (diferensial) ialah fungsi lain dari suatu fungsi sebelumnya, misalkan fungsi f menjadi f’ yang memiliki nilai tidak beraturan. Rumus Dasar Turunan dari Turunan Fungsi Aturan-aturan dalam turunan fungsi ialah: f(x), menjadi f'(x) = 0 Apabila f(x) = x, maka f’(x) = 1 Aturan pangkat : apabila f(x) = x n , maka f’(x) = n X  n – 1 Aturan kelipatan konstanta : apabila (kf) (x) = k. f’(x) Aturan rantai : apabila ( f o g ) (x) = f’ (g (x)). g’(x)) ...

KEKONTINUAN PADA SUATU TITIK Konsep limit, dimana eksitensi (keberadaan) nilai limit fungsi di suatu titik tidak tergantung kepada nilai fungsinya dititik tersebut Tidak mempersoalkan apakah fungsi  terdefinisi dititik Sekarang akan ditinjau hubungan limit fungsi dengan nilai fungsinya disatu titik. Jika limit fungsi  ,  dititik adalah  sendiri dikatakan bahwa fungsi  kontinu dititik  DEFINISI (KEKONTINUAN) Suatu fungsi   dikatakan kontinu dititik   jika Definisi di atas menjelaskan bahwa sebuah fungsi  d ikatakan kontinu dititik    jika memenuhi ketiga syarat berikut :        catatan : jika salah satu syarat kekontinuan diatas tidak dipenuhi, dikatakan fungsi  "tidak kontinu" diskontinu dititik tersebut contoh soal : Gambar di samping menunjukkan grafik fungsi   . Dimana sajakah   tidak kontinu?mengapa? pembahasan fungs...

Bilangan Euler atau e = 2,7182818284... merupakan suatu konstanta dalam matematika dan merupakan basis dari logaritma natural Bilangan e ini sering juga disebut sebagai konstanta napier. seorang atas ahli matematika. Skotlandia yang merumuskan konsep logaritma Teorema berikut ini sangat bermanfaat untuk menyelesaikan soal-soal hitung limit yang berkaitan dengan bilangan Euler. Tentukan Penyelesaian Apabila berturut-turut diambil     dan  maka     Berdasarkan teorema di atas diperoleh sumber : https://www.slideshare.net/rukmonobudi/bilangan-euler https://kalkulus.mipa.ugm.ac.id/single/teorema-limit-bilangan-euler/

Pengertian Limit Fungsi Limit merupakan sebuah konsep  matematika  dimana sesuatu dikatakan “hampir” atau “mendekati” nilai suatu bilangan tertentu. Limit dapat berupa sebuah fungsi yang kodomainnya “hampir” atau “mendekati” nilai suatu bilangan asli tertentu . Sifat-sifat Limit Jika n bilangan bulat positif, k konstanta, f dan g adalah fungsi-fungsi yang mempunyai limit untuk x mendekati a , berlaku sebagai berikut : Mencari Nilai Limit 1.     Metode substitusi Metode ini dilakukan dengan mensubstitusi langsung nilai kedalam fungsi  f(x) . Contoh Soal: 2.     Metode pemfaktoran Jika pada metode substitusi menghasilkan suatu nilai bentuk tak tentu seperti:            maka fungsi tersebut harus difaktorkan terlebih dahulu, kemudian                 bisa disubstitusikan.          Contoh Soal: ...

PENGERTIAN FUNGSI Fungsi adalah : jenis khusus dari relasi , Fungsi f dari X ke Y adalah relasi dari X ke Y yang mempunyai sifat : Domain dari f adalah X Jika (x,y), (x,y)’ Î f, maka y = y’ Notasi :                          f : X à Y Misalkan A dan B merupakan himpunan. Suatu fungsi f dari A ke B merupakan sebuah aturan yang mengkaitkan satu (tepat satu) unsur di B untuk setiap unsur di A. Kita dapat menuliskan f(a) = b, jika b merupakan unsur di B yang dikaitkan oleh f untuk suatu a di A. Ini berarti bahwa jika f(a) = b dan f(a) = c maka b = c. Jika f adalah fungsi dari himpunan A ke himpunan B, kita dapat menuliskan dalam bentuk : f : A → B artinya f meme...